4.7. Сводные таблицы истинности
Для установления истинности формул, состоящих только из двух простых суждений, целесообразно использовать следующую сводную таблицу истинности:
р q ┐р ┐q p Λ q p V q p Ý q p → q p ← q p ↔ q

Для логических формул, состоящих из трех простых суждений, сводная таблица истинности принимает следующий вид:

В этой таблице отсутствуют все виды условных суждений (импликативные, репликативные и эквивалентные), поскольку в них выражается специфика только бинарных отношений — отношений между двумя суждениями.
Приведем пример исчисления истинности суждения с помощью процедур логики высказываний. Рассмотрим следующее высказывание: «Если человеком совершено преступное деяние, то его следует привлечь к суду, но сейчас привлечь гражданина М. к суду невозможно. Следовательно, он не совершил никаких преступных деяний». Обозначим:
суждение " человеком совершено преступное деяние" — р;
суждение " его следует привлечь к суду" — q;
суждение «привлечь гражданина М. к суду невозможно» — ┐q;
суждение «гражданин М не совершал преступных деяний» — ┐р.
Тогда логическая формула данного суждения принимает следующий вид:
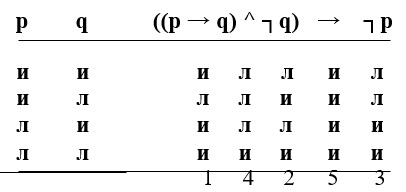
((p → q) ^ ┐q) → ┐р
В этой формуле только два простых суждения. Следовательно, в соответствующей ей таблице истинности должно быть всего четыре строки:
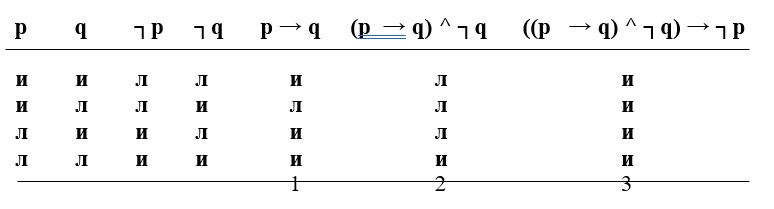
Можно вместо такого «поэтапного» исчисления истинности формулы решать поставленную задачу и более рациональным образом: