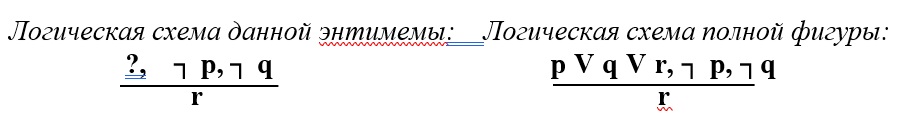9.4. Разделительно-категорическое умозаключение

Разделительно-категорическое умозаключение состоит из двух посылок и заключения: первая (большая) посылка — разделительное суждение, а меньшая посылка и заключение являются категорическими суждениями. Различают только две фигуры разделительно-категорического умозаключения: утверждающе-отрицающий модус (modus ponendo-tollens) и отрицающе- утверждающий (modus tollendo-ponens). Оба модуса правильные.

Логическая схема утверждающе-отрицающего модуса:

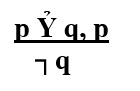
Логическая формула:

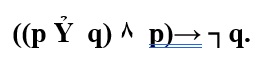
Вывод по данному модусу признается правильным, если первая посылка есть суждение строгой дизъюнкции, т. е. содержащиеся в ней суждения должны исключать друг друга.

Пример:

Приговоры могут быть либо обвинительными либо оправдательными.
По делу М. вынесен обвинительный приговор.
Следовательно, М. не оправдан.

Логическая схема отрицающе-утверждающего модуса:

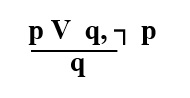
Его логическая формула:

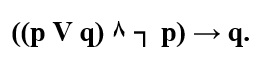
Вывод по данному модусу признается правильным, если в большей посылке модуса перечислены все возможные альтернативы.

Пример:

Приговоры могут быть либо обвинительными, либо оправдательными.

По делу М. не вынесен обвинительный приговор.

Следовательно, М. судом оправдан.

Число альтернатив в разделительной посылке может быть и больше двух. В качестве примера восстановим энтимему, которую представляет собой стихотворение Ф. Тютчева, в полную фигуру разделительно-категорического умозаключения:

Умом Россию не понять, Аршином общим не измерить:
У ней особенная стать -
В Россию можно только верить.

В данном умозаключении пропущена большая посылка: «Страны можно пытаться либо понять, либо измерить, либо остается в них верить». Дополним стихотворение этой посылкой. Тогда заключение Ф. Тютчева о том, что «В Россию можно только верить» следует признать правильным, поскольку данную энтимему удалось представить в виде правильного отрицающе- утверждающнего модуса разделительно-категорического умозаключения, в большей посылке которого перечислены все возможные в данном случае альтернативы.